CLASE 1.-
1.- PROPIEDADES DE LOS NUMERO ENTEROS.
1.- PROPIEDADES DE LOS NUMERO ENTEROS.
Los
números enteros al igual que los números naturales cumplen con ciertas
características que nosotros les llamaremos propiedades, por ejemplo cuando nos
preguntan sobre una persona a la que nosotros conocemos y alguien quiere saber
cómo es esa persona nos empieza a preguntar sobre sus características entonces,
supongamos que alguien quiere saber de los enteros y para esos nos pide sus
características.
Anteriormente se vio que los números naturales tienen ciertas características, se representan con una "N" y como es una colección de números es un
conjunto que lo podemos escribir de la siguiente manera:
N= {1, 2,
3,…}
Pero también se sabe que estos números tienen reflejados a los que les llamamos negativos
y tendrán signo (-), los cuales junto con los naturales y el origen (0) les
llamaremos enteros el cual como también es una colección de números es un
conjunto que lo escribiremos con la letra Z, entonces el conjunto de los enteros lo
podemos escribir como:
Z = {…,
-3, -2, -1, 0, 1, 2, 3,…}
De manera ilustrativa se tiene:
Pero
vemos que los naturales están dentro de los enteros entonces diremos que: 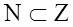 que quiere decir que los naturales son un
subconjunto de los enteros es decir todo número natural es entero.
que quiere decir que los naturales son un
subconjunto de los enteros es decir todo número natural es entero.
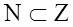 que quiere decir que los naturales son un
subconjunto de los enteros es decir todo número natural es entero.
que quiere decir que los naturales son un
subconjunto de los enteros es decir todo número natural es entero.
Ahora
los reflejados de los naturales son negativos que también están en los enteros, pongamos el nombre de enteros negativos,
y ¿Cómo les pondremos a los naturales que están dentro de los enteros? Como tienen
signo positivo, los llamaremos enteros positivos. Y el cero?
Pero los
negativos son también es un conjunto
porque son colección de números:
Los positivos también son un conjunto y son los mismos que los naturales:
Los positivos también son un conjunto y son
los mismos que los naturales:
¿Con que
letra los representáremos?
Luego
tendremos que si juntamos todos los conjuntos nos hace falta el cero, entonces
lo escribimos a él solo, pero en matemáticas existe un símbolo de la forma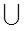 para escribir unión por tanto escribiremos al
conjunto de los enteros como:
para escribir unión por tanto escribiremos al
conjunto de los enteros como:
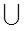 para escribir unión por tanto escribiremos al
conjunto de los enteros como:
para escribir unión por tanto escribiremos al
conjunto de los enteros como:
Pero
cuales son las características de estos números?
Busquemos
algunas propiedades.
Veamos
como son los enteros cuando se suman.
PROPIEDADES DE LA SUMA DE NÚMEROS
ENTEROS
Propiedad de Cierre:
El resultado de
sumar dos números enteros es otro número entero.
Ejemplo: 3 + (−5) 

Propiedad Asociativa:
El modo de agrupar los sumandos no varía el resultado.
(a + b) + c = a + (b + c); a, b, c 

Ejemplo:
(2 + 3) + (− 5) = 2 + [3 + (− 5)]
5 − 5 = 2 + (− 2)
0 = 0
Propiedad Conmutativa:
El orden de los sumandos no cambia la suma.
a + b = b + a; a, b 

Ejemplo:
2 + (− 5) = (− 5) + 2 = − 3,
Propiedad de Elemento identidad:
El 0 es el elemento
identidad de la suma porque todo número sumado con él da el mismo número.
a + 0 = a
Ejemplo:
(−5) + 0 = − 5
Propiedad de Inverso Aditivo
Dos números son opuestos si al sumarlos
obtenemos como resultado el cero.
Ejemplo:
5 + (−5) = 0
El opuesto del opuesto de un número es igual
al mismo número.
− (−5) = 5;
-(-a) = a.
PROPIEDADES DE LA RESTA DE NÚMEROS ENTEROS
Propiedad de Cierre.
La resta dos números enteros es otro número entero.
Ejemplo:
10 − (−5)= 15.
No es Conmutativa:
5 − 2 ≠ 2 – 5
PROPIEDADES DE LA MULTIPLICACIÓN DE NÚMEROS ENTEROS
Propiedad de Cierre:
El resultado de multiplicar dos números enteros es
otro número entero.
Ejemplo:
2 · (−5) = -10
Propiedad Asociativa:
El modo de agrupar los factores no varía el
resultado.
Si a, b y c son números enteros cualesquiera,
se cumple que:
Ejemplo:
(2 · 3) · (−5) = 2· [(3 · (−5)]
6 · (−5) = 2 · (−15)
-30 = -30
Propiedad Conmutativa:
El orden de los factores no varía el producto.
a· b = b · a; a, b 

Ejemplo:
2 · (−5) = (−5) · 2
-10 = -10
Elemento identidad:
El 1 es el elemento identidad de la multiplicación porque todo número multiplicado
por él da el mismo número.
Ejemplo:
(−5)· 1 = (−5)
No
cumple con la propiedad del elemento inverso multiplicativo.
DISTRIBUTIVA: (SUMA Y PRODUCTO).
El producto
de un número por una suma es igual a la suma de los productos de dicho número
por cada uno de los sumandos.
a· (b + c) = a · b + a · c; a, b, c 

Ejemplo:
(−2)· (3 + 5) = (−2) · 3 + (−2) · 5
(−2)· 8 =- 6 - 10
-16 = -16
FACTOR COMÚN:
Es el proceso inverso a la propiedad distributiva.
Si varios sumandos tienen un factor común, podemos transformar la suma
en producto extrayendo dicho factor.
a· b + a · c = a · (b + c); a, b, c

Ejemplo:
(−2) · 3 + (−2) · 5 = (−2) · (3 + 5)
PROPIEDADES DE LA DIVISIÓN DE NÚMEROS ENTEROS
No es cerrado:
El resultado de dividir dos números enteros no siempre
es otro número entero.
No es Conmutativo:
a / b ≠ b / a
Ejemplo:
6 / (−2) ≠ (−2) /6.
2.- EXPRESIONES ALGEBRAICAS.-
Cuando construíamos ecuaciones para encontrar la cuarta y la media proporcional, estábamos construyendo expresiones algebraicas, pero ¿qué debemos entender por expresión algebraica?
Diremos que una expresión algebraica es una secuencia de operaciones indicadas entre números y letras.
Por ejemplo:

Las expresiones algebraicas aparecen en muchas situaciones, por ejemplo en geometría las fórmulas de área de un triángulo está dada por A=bh/2 donde b es la base y h es la altura del mismo.
Las ecuaciones diofánticas son otro ejemplo como ya se dijo de expresiones algebraicas.
Construir expresiones algebraicas.
Ya hemos construido expresiones algebraicas antes, cuando escribíamos ecuaciones para encontrar la media y la cuarta proporcional. Ahora construiremos expresiones algebraicas a partir de situaciones más generales.
Ejemplo:
Escriba en una expresión algebraica el siguiente enunciado: Al cuadrado de cierto número se multiplica por cuatro.
Solución:
Como no sabemos qué número es le pondremos un nombre a dicho número, es decir lo representaremos por una letra digamos
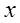 , luego el cuadrado de
, luego el cuadrado de 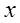 es
es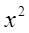 y como al cuadrado hay que multiplicarlo por
y como al cuadrado hay que multiplicarlo por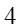 , la expresión algebraica resultante es
, la expresión algebraica resultante es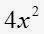 . Note como un enunciado de muchas palabras en álgebra se convierte en unos cuantos símbolos.
. Note como un enunciado de muchas palabras en álgebra se convierte en unos cuantos símbolos.Monomios.
El el monomio es una expresión algebraica que consta de un solo término; por ejemplo los binomios constan de 2 términos, el trinomio consta de 3 y el polinomio consta de 2 o más términos.
Se tiene el siguiente ejemplo:
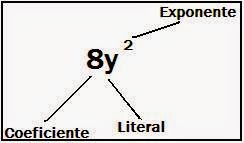
El monomio está compuesto por 3 elementos uno es el:
El Coeficiente: Es el número que multiplica a la literal
Literal: Es la letra que representa una cantidad.
El Exponente: Es la potencia esto significa la cantidad de veces que se va a multiplicar una cantidad, en este caso sería el valor de y se multiplica 2 veces por sí mismo esto es porque el exponente es 2.
Suma o resta de monomios.
Dos monomios se dicen semejantes si tienen la misma parte literal aunque tengan distinto coeficiente.
Ejemplo:
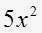 es semejante a
es semejante a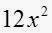 , pero
, pero 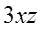 no es semejante a
no es semejante a 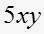 ya que tienen distinta parte literal.
ya que tienen distinta parte literal.Para sumar dos monomios semejantes, se suman los coeficientes y se escribe la misma parte literal.
Para restar dos monomios semejantes, se restan los coeficientes y se escribe la misma parte literal.
Ejemplo:
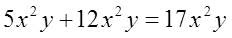
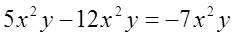
Si los monomios no son semejantes, entonces la suma o resta de ellos se deja indicada.
Ejemplo:
Sume,
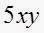 con
con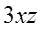
Resultado:
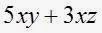
Ahora reste
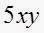 de
de 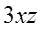 , convénzase de que el resultado es
, convénzase de que el resultado es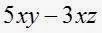
Multiplicación y división de monomios.
Primero recordaremos que si a y b son números reales cualesquiera y m, n son enteros, entonces
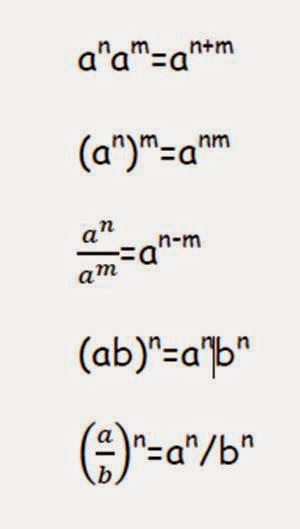
Note que
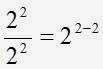 , pero como
, pero como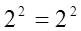 , se tiene que
, se tiene que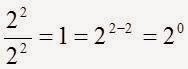 .
.En general si a es cualquier número real distinto de cero, se tiene que
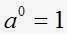
Además para cualquier número real
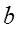 , se tiene
, se tiene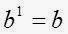 .
.Las afirmaciones anteriores son conocidas como reglas de los exponentes.
Para multiplicar monomios, se multiplican los coeficientes y luego las partes literales aplicando las reglas de los exponentes.
Ejemplo:
Multiplicar
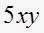 por
por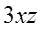
Solución:
Escribimos
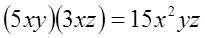
Para dividir monomios, se dividen los coeficientes y luego las partes literales aplicando las reglas de los exponentes.
Ejemplo:
Dividir
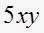 por
por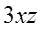
Solución:
Escribimos,
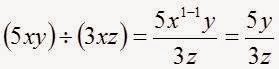















No hay comentarios:
Publicar un comentario